1.1: Added the ability to indicate left or right limit for each variable.
1.2: Added some tests that will eliminate some but not all undefined limits.

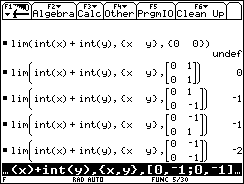
lim(expr,VarList,LimitPoints)
expr: An EXPR of zero or more variables.
VarList: A LIST of the limit variables.
LimitPoints: Can be type NUM, LIST, or MAT:
- NUM- Each variable will be evaluated to this same limit from the left and right. I.e. lim(a+b+c,{a,b,c},0)=lim(a,b,c)->(0,0,0)(a+b+c).
- LIST- List of the limit points corresponding to the order of the limit variables in VarList. I.e. lim(a+b+c,{a,b,c},{0,0,0})=lim(a,b,c)->(0,0,0)(a+b+c).
- MAT- Left or right limits can be selected for each variable by changing LimitPoints to an Nx2 MAT, where [n,1] is the limit point and [n,2] is either 0, -1, or 1 to indicate both, left, or right respectively. I.e. lim(a+b+c,{a,b,c},[0,-1;0,0;0,1])=lim(a,b,c)->(0-,0,0+)(a+b+c).
NOTE: This function calls the built-in limit() function n2 times, where n is the number of variables in VarList, so each additional variable in the expression will significantly add to the amount of time it takes to evaluate it. The reason for this is that I cannot come up with a routine that will prove or disprove a limit so I try to eliminate some invalid limits by changing the order in which variables are evaluated. Ideally this would be n! evaluations so n2 is a compromise.
Return Value:
This function returns the limit of the multivariable expression.
Example:
1. lim(x2y/(x4+y2),{x,y},{0,0))
0
. lim(x2y/(x4+y2),{x,y},{0,0))|y=x2
1/2
Therefore the limit does not exist.
2. lim(x2+y2,{x,y},{2,3})
13
3. lim(ln(x)+ln(y)+ln(z),{x,y,z},{0,0,0}) [Limit as (x,y,z)
-> (0,0,0)]
undef
lim(ln(x)+ln(y)+ln(z),{x,y,z},[0,1;0,1;0,1])
[Limit as (x,y,z) -> (0+,0+,0+)]
-infinity